31 Loading and Visualising the Historical Boundaries

Let’s imagine we’ve been told that the historical boundaries have been based on groups of LSOAs. We’ve been given a list of the LSOAs that belong to each dispatcher, but we only have a standard file of all LSOAs in our region. How can we turn our lists of LSOAs and this file into something to help us visualise the boundaries, and later start to alter the boundaries to try out different solutions?

Note

There are other ways in which you may get the boundaries.

You may be able to find a shapefile, geojson or geopackage file defining the boundaries.
You may draw the boundaries in another tool, like

31.1 Our region

We’re going to work with our Birmingham region again. We first worked with this in the section of the book covering travel times; we may return to this travel time data in a later chapter of this part.

To start with, let’s just visualise our wider region.

import geopandas

lsoa_geojson_path = 'https://github.com/hsma-programme/h6_3c_interactive_plots_travel/raw/main/h6_3c_interactive_plots_travel/example_code/LSOA_2011_Boundaries_Super_Generalised_Clipped_BSC_EW_V4.geojson'

lsoa_boundaries = geopandas.read_file(lsoa_geojson_path)

Let’s now filter this down to just our region.

xmin, xmax = 370000, 420000
ymin, ymax = 250000, 310000

bham_region = lsoa_boundaries.cx[xmin:xmax, ymin:ymax]

bham_region.plot(
    figsize=(10,7),
    edgecolor='black',
    color="cyan"
    )

Tip

There are other ways you could conduct this initial filtering - for example, using a list of LSOAs you need to cover, or a filter

Straight away we can see that there are a very large number of LSOAs in our problem, with a lot of variation in the area of each LSOA.

We’ll start with the split of our LSOAs by their overarching dispatch center.

We’ve been told that our dispatch centres are split based on the wider region name. Here, we’d visualised these names.

import matplotlib.pyplot as plt

bham_region.head()

bham_region["region"] = bham_region["LSOA11NM"].str[:-5]

fig, ax = plt.subplots(figsize=(10,7))

ax = bham_region.plot(
    ax=ax,
    edgecolor='black',
    column="region",
    legend=True,
    cmap="tab20",
    legend_kwds={'loc':'center left', 'bbox_to_anchor':(1.2, 0.5)}
    )

# Add a dark background to our plotted region
ax.set_facecolor('black')
fig.patch.set_facecolor('black')

# Add a label per region for easier crossreferencing
# particularly where colours aren't very distinct
one_row_per_region = bham_region.groupby('region').head(1)

for x, y, label in zip(one_row_per_region.geometry.centroid.x, one_row_per_region.geometry.centroid.y, one_row_per_region.region):
    ax.annotate(label, xy=(x, y), xytext=(0, 0), textcoords="offset points", color="white",
    fontweight="bold")

ax.axis('off')

/home/sammi/.local/lib/python3.10/site-packages/geopandas/geodataframe.py:1528: SettingWithCopyWarning:


A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy

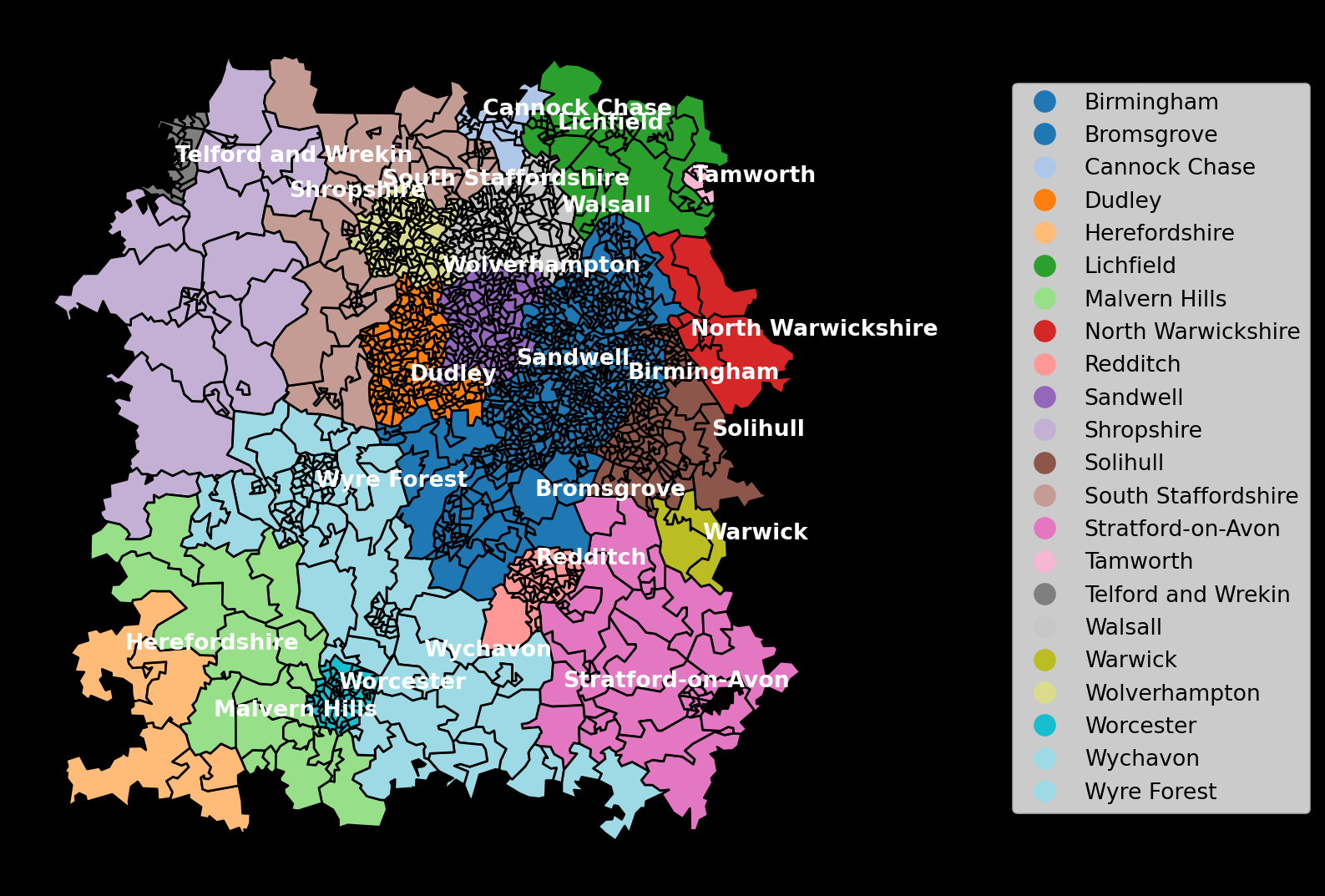
We’ve been told that the regions are as follows:

Centre 1

Dispatcher 1: Telford and Wrekin; Shropshire
Dispatcher 2: Cannock Chase; Lichfield; Tamworth
Dispatcher 3: South Staffordshire; Walsall
Dispatcher 4: Wolverhampton
Dispatcher 5: Dudley; Sandwell
Dispatcher 6: Birmingham
Dispatcher 7: Solihull; North Warwickshire

Centre 2

Dispatcher 1: Bromsgrove
Dispatcher 2: Wyre Forest
Dispatcher 3: Wychavon; Worcester
Dispatcher 4: Malvern Hills; Herefordshire
Dispatcher 5: Redditch; Stratford-on-Avon; Warwick

This information has been given to us in a dataframe; let’s import and inspect this, then join it to our other data.

import pandas as pd

boundary_allocations_df = pd.read_csv("boundary_allocations.csv")
boundary_allocations_df.head()

	Region	Centre	Dispatcher
0	Telford and Wrekin	Centre 1	1
1	Shropshire	Centre 1	1
2	Cannock Chase	Centre 1	2
3	Lichfield	Centre 1	2
4	Tamworth	Centre 1	2

If we join this to our boundary data, with the geodataframe on the left of the merge, we can then access the data about the dispatchers and centers as variables we can plot.

First, let’s do the join and view the resulting dataframer which will have the additional columns. As the original dataframe only contains separate columns for center and dispatcher, we will first create an additional column that joins the two together.

bham_region = pd.merge(
    bham_region,
    boundary_allocations_df,
    left_on="region",
    right_on="Region",
    how="left"
)

bham_region["centre_dispatcher"] = bham_region["Centre"].astype("str") + '-' + bham_region["Dispatcher"].astype("str")

bham_region.head()

	FID	LSOA11CD	LSOA11NM	LSOA11NMW	BNG_E	BNG_N	LONG	LAT	GlobalID	geometry	region	Region	Centre	Dispatcher	centre_dispatcher
0	8649	E01008881	Birmingham 067A	Birmingham 067A	412690	285438	-1.81463	52.46675	f79cd8fb-0cf2-4c84-b07c-55bffcf379bb	POLYGON ((413040.413 285809.794, 413145.440 28...	Birmingham	Birmingham	Centre 1	6	Centre 1-6
1	8650	E01008882	Birmingham 066A	Birmingham 066A	411772	285390	-1.82814	52.46634	e7835311-f105-4c92-acae-ecd5255ce534	POLYGON ((412233.657 285480.231, 412255.373 28...	Birmingham	Birmingham	Centre 1	6	Centre 1-6
2	8651	E01008883	Birmingham 078A	Birmingham 078A	412121	285001	-1.82302	52.46283	29dbcbc2-4a29-4bb1-addb-42b37d91c647	POLYGON ((412775.838 285204.808, 412575.845 28...	Birmingham	Birmingham	Centre 1	6	Centre 1-6
3	8652	E01008884	Birmingham 078B	Birmingham 078B	411241	284712	-1.83598	52.46025	df5a2350-a102-4ecc-b028-5a0bbeded198	POLYGON ((411803.096 284902.674, 411563.054 28...	Birmingham	Birmingham	Centre 1	6	Centre 1-6
4	8653	E01008885	Birmingham 076A	Birmingham 076A	413207	284818	-1.80704	52.46116	13a855fc-fa09-42a5-a05e-947fcd141ce4	POLYGON ((413417.353 284803.764, 413034.282 28...	Birmingham	Birmingham	Centre 1	6	Centre 1-6

Let’s first just visualise the split across our dispatching centres by plotting the center column.

ax = bham_region.plot(
    edgecolor='black',
    column="Centre",
    legend=True,
    legend_kwds={'loc':'center left', 'bbox_to_anchor':(1.2, 0.5)}
    )

ax.axis('off')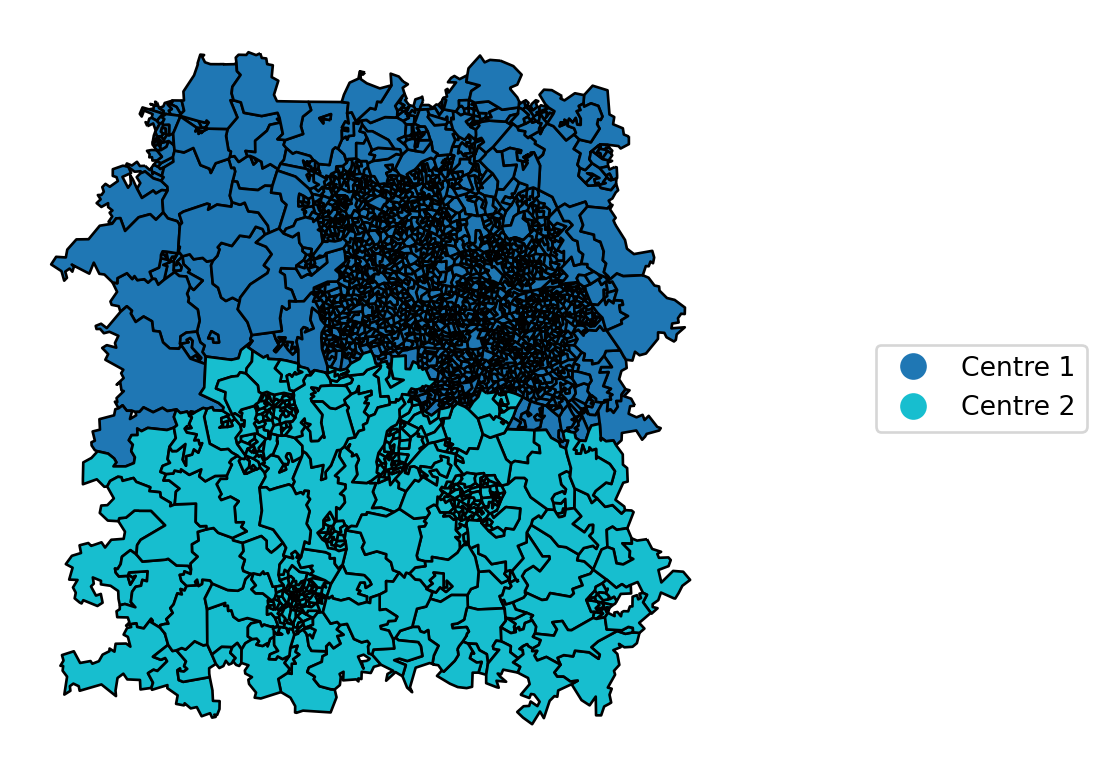

Then we’ll visualise the split per dispatcher, using our new column to avoid issues with dispatcher numbers being duplicated across centres.

ax = bham_region.plot(
    edgecolor='black',
    column="centre_dispatcher",
    legend=True,
    cmap="tab20",
    legend_kwds={'loc':'center left', 'bbox_to_anchor':(1.2, 0.5)}
    )

ax.axis('off')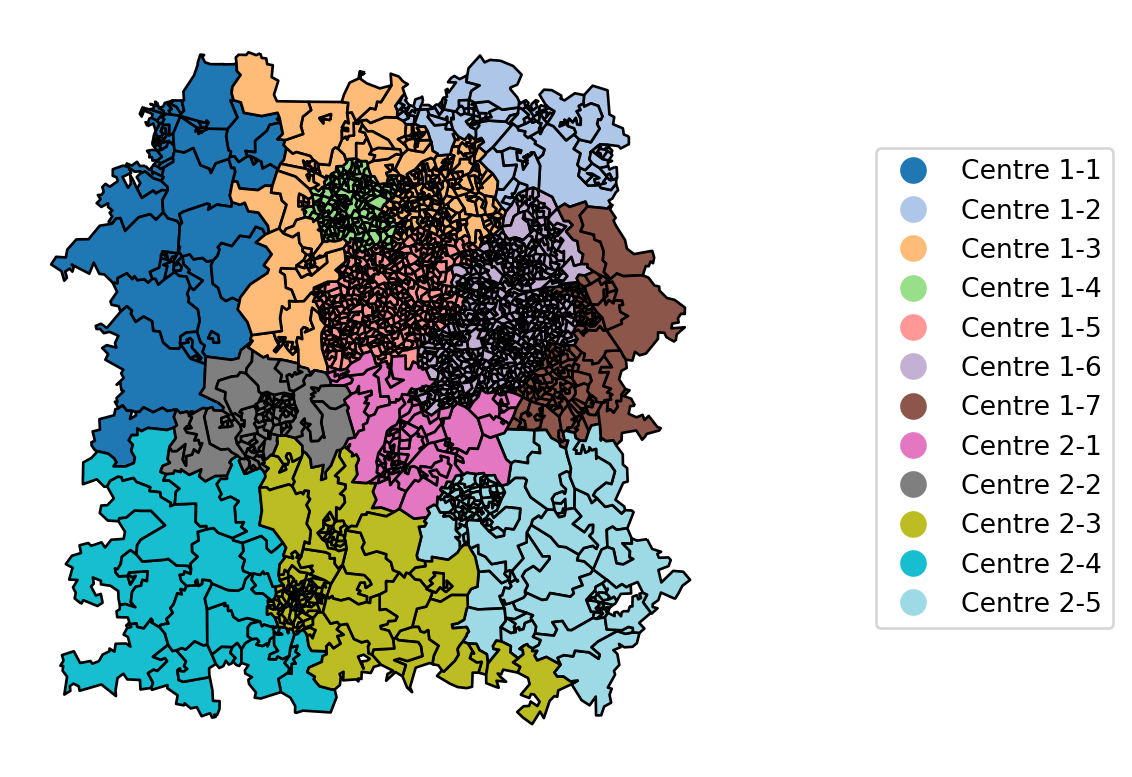

Finally, let’s demonstrate how we could overlay the plot by dispatcher with something that highlights the per-centre boundary as well.

To do this, we will have to merge all of the polygons into a single large polygon. This will give us a brand new dataframe with just two rows referencing the two large polygons; we will view this at the end.

GenAI Alert - This code was modified from a suggested approach provided by ChatGPT

# Group by the specified column
grouped_centre_gdf = bham_region.groupby('Centre')

# Create a new GeoDataFrame for the boundaries of each group
boundary_list = []

for group_name, group in grouped_centre_gdf:
    # Combine the polygons in each group into one geometry
    combined_geometry = group.unary_union

    # Get the boundary of the combined geometry
    boundary = combined_geometry.boundary

    # Add the boundary geometry and the group name to the list
    boundary_list.append({'group': group_name, 'boundary': boundary})

# Create a GeoDataFrame from the list of boundaries
grouped_centre_gdf_boundary = geopandas.GeoDataFrame(boundary_list, geometry='boundary', crs=bham_region.crs)

grouped_centre_gdf_boundary.head()

	group	boundary
0	Centre 1	MULTILINESTRING ((366838.095 273147.999, 36728...
1	Centre 2	MULTILINESTRING ((376328.508 242672.351, 37647...

Finally, we’ll repeat our per-dispatcher

ax = bham_region.plot(
    edgecolor='black',
    column="centre_dispatcher",
    legend=True,
    cmap="tab20",
    legend_kwds={'loc':'center left', 'bbox_to_anchor':(1.2, 0.5)}
    )

grouped_centre_gdf_boundary.plot(
    edgecolor='red',
    ax=ax,
    linewidth=2
)

ax.axis('off')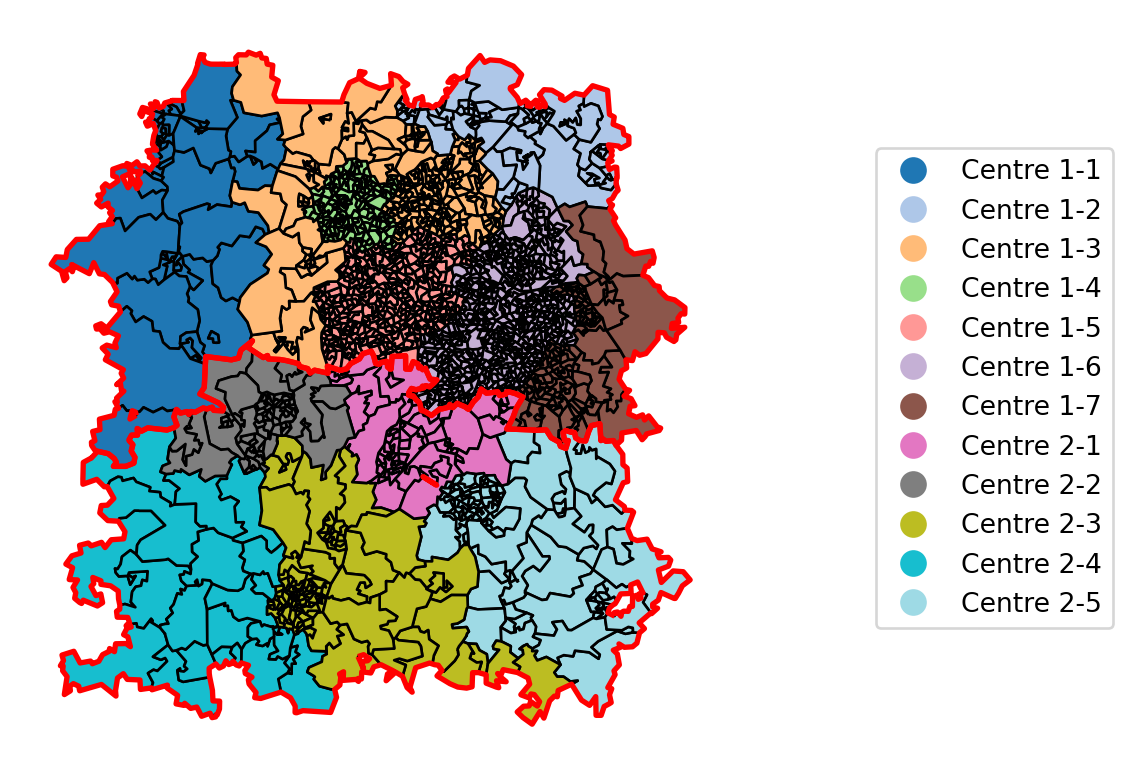

31.2 Bringing in historical demand data

Finally, let’s bring in some historical demand data to see if we can spot any obvious issues.

First, so we can overlay both the centre boundaries and the per-dispatcher boundaries, we’ll repeat our earlier process to create a geodataframe with a single row and a single polygon per dispatcher.

# Group by the specified column
grouped_dispatcher_gdf = bham_region.groupby("centre_dispatcher")

# Create a new GeoDataFrame for the boundaries of each group
boundary_list = []

for group_name, group in grouped_dispatcher_gdf:
    # Combine the polygons in each group into one geometry
    combined_geometry = group.unary_union

    # Get the boundary of the combined geometry
    boundary = combined_geometry.boundary

    # Add the boundary geometry and the group name to the list
    boundary_list.append({'group': group_name, 'boundary': boundary})

# Create a GeoDataFrame from the list of boundaries
grouped_dispatcher_gdf_boundary = geopandas.GeoDataFrame(boundary_list, geometry='boundary', crs=bham_region.crs)

grouped_dispatcher_gdf_boundary.head()

	group	boundary
0	Centre 1-1	MULTILINESTRING ((368935.969 274516.594, 36824...
1	Centre 1-2	LINESTRING (412258.535 300984.197, 411756.668 ...
2	Centre 1-3	LINESTRING (381775.908 282326.500, 380577.001 ...
3	Centre 1-4	LINESTRING (388885.341 295185.385, 388630.406 ...
4	Centre 1-5	LINESTRING (388258.095 285110.427, 388666.258 ...

demand = pd.read_csv("demand_pop_bham.csv")

bham_region = bham_region.merge(demand, on="LSOA11CD")

ax = bham_region.plot(
    edgecolor='black',
    column="demand",
    cmap="Blues",
    legend=True,
    linewidth=0.3
    )

grouped_dispatcher_gdf_boundary.plot(
    edgecolor='purple',
    ax=ax,
    linewidth=1.5
)

grouped_centre_gdf_boundary.plot(
    edgecolor='red',
    ax=ax,
    linewidth=2.5
)

ax.axis('off')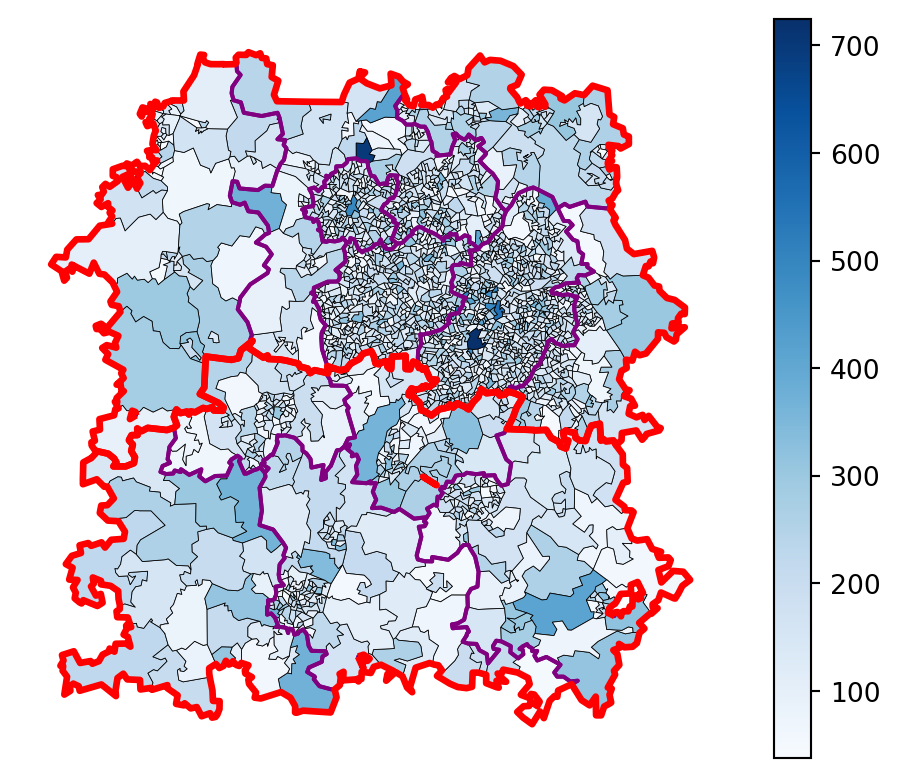

31.3 Looking at the current balance of incidents across the region

The demand dataset provided gives us the total number of incidents our dispatchers have dealt with per region per year. Let’s do a bit of merging and exploratory data analysis to see how this varied historically, and so we can start to think about what would be a target level of demand for each region.

First let’s look at the per-centre rates.

grouped_by_centre = bham_region.groupby('Centre')[['demand']].sum()
grouped_by_centre['difference_from_average'] = (grouped_by_centre['demand'] - grouped_by_centre['demand'].mean()).astype('int')
grouped_by_centre

	demand	difference_from_average
Centre
Centre 1	277146	110663
Centre 2	55820	-110663

And now by dispatcher

grouped_by_dispatcher = bham_region.groupby('centre_dispatcher')[['demand']].sum()
mean_demand = grouped_by_dispatcher['demand'].mean()
print(f"The demand, averaged across {len(bham_region['centre_dispatcher'].unique())} regions, is {mean_demand:.0f} incidents per year")

The demand, averaged across 12 regions, is 27747 incidents per year

grouped_by_dispatcher['difference_from_mean'] = (grouped_by_dispatcher['demand'] - mean_demand).astype('int')
grouped_by_dispatcher

	demand	difference_from_mean
centre_dispatcher
Centre 1-1	7600	-20147
Centre 1-2	12825	-14922
Centre 1-3	36084	8336
Centre 1-4	26690	-1057
Centre 1-5	63379	35631
Centre 1-6	109387	81639
Centre 1-7	21181	-6566
Centre 2-1	9630	-18117
Centre 2-2	9429	-18318
Centre 2-3	16699	-11048
Centre 2-4	4217	-23530
Centre 2-5	15845	-11902

print(f"The average difference from the mean across all regions is {abs(grouped_by_dispatcher['difference_from_mean']).mean():.1f}")

The average difference from the mean across all regions is 20934.4

import plotly.express as px

px.bar(grouped_by_dispatcher.reset_index(), x="centre_dispatcher", y="difference_from_mean")

No wonder our dispatchers are struggling - there are huge discrepancies in the demand they have been responsible for.

So what are we going to do about it?

Unlike in our travel time location work in the location allocation chapter, where we initially focussed on minimize the average travel time or population-weighted travel time, here we instead want to minimize the difference between the demand for each region going forward - so let’s move onto the next chapter and explore how we will do that.